#include <reducednewtonalgorithmwithinverse.h>

Inheritance diagram for DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >:

Public Member Functions
	ReducedNewtonAlgorithmWithInverse (PROBLEM OP, ReducedProblemInterface< PROBLEM, VECTOR > S, ParameterReader &param_reader, DOpEExceptionHandler< VECTOR > Except=NULL, DOpEOutputHandler< VECTOR > Output=NULL, int base_priority=0)

	~ReducedNewtonAlgorithmWithInverse ()

virtual int	Solve (ControlVector< VECTOR > &q, double global_tol=-1.)

Public Member Functions inherited from DOpE::ReducedNewtonAlgorithm< PROBLEM, VECTOR >
	ReducedNewtonAlgorithm (PROBLEM OP, ReducedProblemInterface< PROBLEM, VECTOR > S, ParameterReader &param_reader, DOpEExceptionHandler< VECTOR > Except=NULL, DOpEOutputHandler< VECTOR > Output=NULL, int base_priority=0)

	~ReducedNewtonAlgorithm ()

double	NewtonResidual (const ControlVector< VECTOR > &q)

Public Member Functions inherited from DOpE::ReducedAlgorithm< PROBLEM, VECTOR >
	ReducedAlgorithm (PROBLEM OP, ReducedProblemInterface< PROBLEM, VECTOR > S, ParameterReader &param_reader, DOpEExceptionHandler< VECTOR > Except=NULL, DOpEOutputHandler< VECTOR > Output=NULL, int base_priority=0)

	~ReducedAlgorithm ()

virtual void	ReInit ()

virtual void	SolveForward (ControlVector< VECTOR > &q)

virtual void	CheckGrads (double c, ControlVector< VECTOR > &q, ControlVector< VECTOR > &dq, unsigned int niter=1, double eps=1.)

virtual void	FirstDifferenceQuotient (double exact, double eps, const ControlVector< VECTOR > &q, const ControlVector< VECTOR > &dq)

virtual void	CheckHessian (double c, ControlVector< VECTOR > &q, ControlVector< VECTOR > &dq, unsigned int niter=1, double eps=1.)

virtual void	SecondDifferenceQuotient (double exact, double eps, const ControlVector< VECTOR > &q, const ControlVector< VECTOR > &dq)

DOpEExceptionHandler< VECTOR > *	GetExceptionHandler ()

DOpEOutputHandler< VECTOR > *	GetOutputHandler ()

Static Public Member Functions
static void	declare_params (ParameterReader &param_reader)

Static Public Member Functions inherited from DOpE::ReducedNewtonAlgorithm< PROBLEM, VECTOR >
static void	declare_params (ParameterReader &param_reader)

Static Public Member Functions inherited from DOpE::ReducedAlgorithm< PROBLEM, VECTOR >
static void	declare_params (ParameterReader &param_reader)

Protected Member Functions
int	SolveReducedLinearSystem (const ControlVector< VECTOR > &q, const ControlVector< VECTOR > &gradient, const ControlVector< VECTOR > &gradient_transposed, ControlVector< VECTOR > &dq)

double	Residual (const ControlVector< VECTOR > &gradient, const ControlVector< VECTOR > &)

Protected Member Functions inherited from DOpE::ReducedNewtonAlgorithm< PROBLEM, VECTOR >
virtual int	ReducedNewtonLineSearch (const ControlVector< VECTOR > &dq, const ControlVector< VECTOR > &gradient, double &cost, ControlVector< VECTOR > &q)

Protected Member Functions inherited from DOpE::ReducedAlgorithm< PROBLEM, VECTOR >
PROBLEM *	GetProblem ()

const PROBLEM *	GetProblem () const

const ReducedProblemInterface < PROBLEM, VECTOR > *	GetReducedProblem () const

ReducedProblemInterface < PROBLEM, VECTOR > *	GetReducedProblem ()

int	GetBasePriority () const

Detailed Description

template<typename PROBLEM, typename VECTOR>
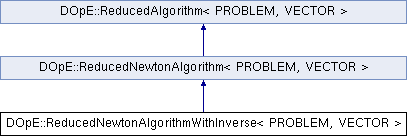
class DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >

This class provides a solver for equality constrained optimization problems in reduced form, i.e., the dependent variable is assumed to be eliminated by solving the equation. I.e., we solve the problem min j(q)

This class implements a linesearch newton algorithm where the linear system is solved exactly. This requires that <PROBLEM> posseses a working method PROBLEM::ComputeReducedHessianInverseVector which is reasonable only if the problem has a very simple structure.

Template Parameters

<PROBLEM>	The problem to deal with.
<VECTOR>	The type of Vector used in the ControlVectors

Constructor & Destructor Documentation

template<typename PROBLEM , typename VECTOR >

DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >::ReducedNewtonAlgorithmWithInverse	(	PROBLEM *	OP,
		ReducedProblemInterface< PROBLEM, VECTOR > *	S,
		ParameterReader &	param_reader,
		DOpEExceptionHandler< VECTOR > *	Except = `NULL`,
		DOpEOutputHandler< VECTOR > *	Output = `NULL`,
		int	base_priority = `0`
	)

The constructor for the algorithm

Parameters

OP	A pointer to the problem container
S	The reduced problem. This object handles the equality constraint. For the interface see ReducedProblemInterface.
param_reader	A parameter reader to access user given runtime parameters.
Except	The DOpEExceptionHandler. This is used to handle the output by all exception.
Output	The DOpEOutputHandler. This takes care of all output generated by the problem.
base_priority	An offset for the priority of the output generated by the algorithm.

template<typename PROBLEM , typename VECTOR >

DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >::~ReducedNewtonAlgorithmWithInverse ( )

Member Function Documentation

template<typename PROBLEM , typename VECTOR >

void DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >::declare_params ( ParameterReader & param_reader )

static

Used to declare run time parameters. This is needed to declare all parameters a startup without the need for an object to be already declared.

template<typename PROBLEM , typename VECTOR >

double DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >::Residual	(	const ControlVector< VECTOR > &	gradient,
		const ControlVector< VECTOR > &	gradient_transposed
	)

inlineprotectedvirtual

Evaluates the squared residual, i.e., the scalar product gradient*gradient_transposed

Reimplemented from DOpE::ReducedNewtonAlgorithm< PROBLEM, VECTOR >.

template<typename PROBLEM , typename VECTOR >

int DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >::Solve	(	ControlVector< VECTOR > &	q,
		double	global_tol = `-1.`
	)

virtual

This solves an Optimizationproblem in only the control variable by a newtons method.

Parameters

q	The initial point.
global_tol	An optional parameter specifying the required tolerance. The actual tolerance is the maximum of this and the one specified in the param file. Its default value is negative, so that it has no influence if not specified.

Reimplemented from DOpE::ReducedNewtonAlgorithm< PROBLEM, VECTOR >.

template<typename PROBLEM , typename VECTOR >

int DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >::SolveReducedLinearSystem	(	const ControlVector< VECTOR > &	q,
		const ControlVector< VECTOR > &	gradient,
		const ControlVector< VECTOR > &	gradient_transposed,
		ControlVector< VECTOR > &	dq
	)

protectedvirtual

Solves the linear system corresponding to the unconstrained quadratic model j(q) + j'(q)p + 1/2 p^TH(q)p

The values for j'(q) need to be provided. Here it is assumed that the hessian can be inverted directly!

Parameters

q	The fixed point where j, j' is evaluated and H needs to be calculated.
gradient	The l^2 gradient of the costfunctional at q, i.e., the gradient_i = {q_i} j(q) where q_i denotes the i-th DoF for the control.
gradient_transposed	The transposed of the gradient. This is assumed to be such that if q lives in a Hilbert space Q, then (gradient_transposed,gradient)_{l^2} = \|j'(q)\|_Q^2
dq	The solution of the model minimization, i.e., H(q)dq = - j'(q).

Reimplemented from DOpE::ReducedNewtonAlgorithm< PROBLEM, VECTOR >.

The documentation for this class was generated from the following file:

/afs/math.uni-hamburg.de/users/oa/fmrv001/src/DOpE/ThingsForMaintainer/Releases/dopelib-1.0/DOpEsrc/opt_algorithms/reducednewtonalgorithmwithinverse.h

Public Member Functions

Static Public Member Functions

Protected Member Functions

Detailed Description

template<typename PROBLEM, typename VECTOR> class DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >

Constructor & Destructor Documentation

Member Function Documentation

template<typename PROBLEM, typename VECTOR>
class DOpE::ReducedNewtonAlgorithmWithInverse< PROBLEM, VECTOR >